Kramers–Heisenberg formula

The Kramers-Heisenberg dispersion formula is an expression for the cross section for scattering of a photon by an atomic electron. It was derived before the advent of quantum mechanics by Hendrik Kramers and Werner Heisenberg in 1925,[1] based on the correspondence principle applied to the classical dispersion formula for light. The quantum mechanical derivation was given by Paul Dirac in 1927.[2][3]

The Kramers–Heisenberg formula was an important achievement when it was published, explaining the notion of "negative absorption" (stimulated emission), the Thomas-Reiche-Kuhn sum rule, and inelastic scattering - where the energy of the scattered photon may be larger or smaller than that of the incident photon - thereby anticipating the Raman effect.[4]

Equation

The Kramers-Heisenberg (KH) formula for second order processes is [1] [5]
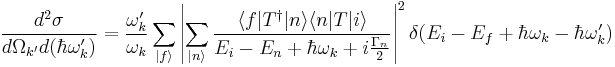
\frac{d^2 \sigma}{d\Omega_{k^\prime}d(\hbar \omega_k^\prime)}=\frac{\omega_k^\prime}{\omega_k}\sum_{|f\rangle}\left | \sum_{|n\rangle} \frac{\langle f | T^\dagger | n \rangle \langle n | T | i \rangle}{E_i - E_n %2B \hbar \omega_k %2B i \frac{\Gamma_n}{2}}\right |^2 \delta (E_i - E_f %2B \hbar \omega_k - \hbar \omega_k^\prime)

It represents the probability of the emission of photons of energy 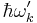\hbar \omega_k^\prime in the solid angle 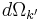d\Omega_{k^\prime} (centred in the 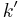k^\prime direction), after the excitation of the system with photons of energy 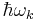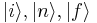\hbar \omega_k. |i\rangle, |n\rangle, |f\rangle are the initial, intermediate and final states of the system with energy 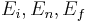E_i , E_n , E_f respectively; the delta function ensures the energy conservation during the whole process. 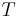T is the relevant transition operator. 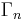\Gamma_n is the instrinsic linewidth of the intermediate state.

References

  1. ^ a b Kramers, H. A.; Heisenberg, W. (Feb 1925). "Über die Streuung von Strahlung durch Atome". Z. Phys. 31 (1): 681–708. Bibcode 1925ZPhy...31..681K. doi:10.1007/BF02980624. http://www.springerlink.com/content/x2x7220805540747. 
  2. ^ Dirac., P. A. M. (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proc. Roy. Soc. Lond. A 114 (769): 243–265. Bibcode 1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039. 
  3. ^ Dirac., P. A. M. (1927). "The Quantum Theory of Dispersion". Proc. Roy. Soc. Lond. A 114 (769): 710–728. Bibcode 1927RSPSA.114..710D. doi:10.1098/rspa.1927.0071. 
  4. ^ Breit, G. (1932). "Quantum Theory of Dispersion". Rev. Mod. Phys. 4 (3): 504–576. Bibcode 1932RvMP....4..504B. doi:10.1103/RevModPhys.4.504. http://link.aps.org/doi/10.1103/RevModPhys.4.504. 
  5. ^ J.J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley (1967), page 56.